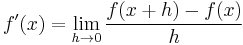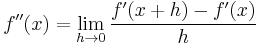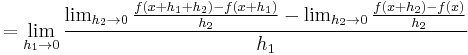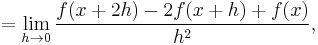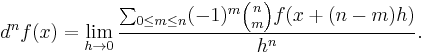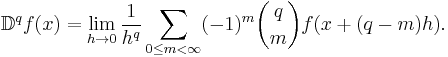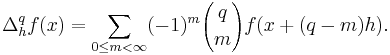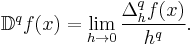Grünwald–Letnikov derivative
In mathematics, the Grünwald–Letnikov derivative is a basic extension of the derivative in fractional calculus, that allows one to take the derivative a non-integer number of times. It was introduced by Anton Karl Grünwald (1838–1920) from Prague, in 1867, and by Aleksey Vasilievich Letnikov (1837-1888) in Moscow in 1868.
Constructing the Grünwald–Letnikov derivative
The formula
for the derivative can be applied recursively to get higher-order derivatives. For example, the second-order derivative would be:
Assuming that the h 's converge synchronously, this simplifies to:
which can be justified rigorously by the mean value theorem. In general, we have (see binomial coefficient):
Formally, removing the restriction that n be a positive integer, it is reasonable to define:
This defines the Grünwald–Letnikov derivative.
Another notation
We may also write the expression more simply if we make the substitution:
This results in the expression:
References
- The Fractional Calculus, by Oldham, K.; and Spanier, J. Hardcover: 234 pages. Publisher: Academic Press, 1974. ISBN 0-12-52555-0-0